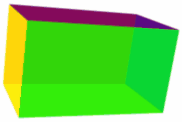
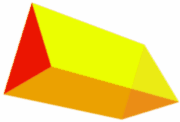
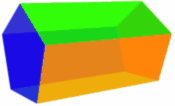
Un
prisma recto es un prisma en el que los bordes de unión y las caras son
perpendiculares a las caras de la base. Esto se aplica si las caras de unión son
rectangulares. Si los bordes de unión y las caras no son perpendiculares a las caras de la base, se llama
prisma oblicuo.
Algunos textos pueden aplicar el término de
prisma rectangular o
prisma cuadrado tanto a un prisma rectangular de lado derecho como a un prisma unilateral cuadrado derecho. El término
prisma uniforme puede utilizarse para un prisma recto con lados cuadrados, ya que tales prismas están en el conjunto de
poliedros uniforme.
Un prisma
n que tiene extremos de
polígonos regulares y caras rectangulares, se acerca un sólido cilíndrico cuando
n tiende a
infinito.
Los prismas rectos con bases regulares y longitudes iguales bordes forman una de las dos series infinitas de poliedros semirregulares, las otras series son los
anti prismas.
Un
paralelepípedo es un prisma de que la base es un
paralelogramo, o equivalentemente un poliedro con seis caras que son todas paralelogramos.
A un prisma rectangular recto también se lo conoce como
cuboides, o informalmente caja rectangular. Un prisma cuadrado derecho es simplemente una caja cuadrada, y también puede ser llamado un
cuboide cuadrado.Los prismas son poliedros que constan de dos caras iguales y paralelas llamadas bases, y de caras laterales que son paralelogramos.
Cada prisma consta de los siguientes elementos:
Bases: son las dos caras iguales y paralelas del prisma, una en la que se apoya y la otra su opuesta. Caras laterales: son las caras que comparten dos de sus lados con las bases. La suma de sus áreas es la superficie lateral del prisma. Aristas: son los lados de las bases y de las caras laterales. Vértices: son los puntos en donde se encuentran cada par de aristas. Altura: es la distancia entre las bases. Diagonales: son los segmentos que unen dos vértices no consecutivos del prisma. Se pueden trazar las diagonales de una cara o entre dos caras.
Volumen
El
volumen de un prisma es el producto del
área de la base por la distancia o altura entre las dos base. Su valor se expresa como:
donde
B es el área de la base y
h es la altura. El volumen de un prisma, cuya base es un
polígono regular de
n lados con una longitud de lado
s, es:
Simetría
El
grupo de simetría de un prisma recto de n lados con la base regular es
Dnh del orden 4
n, excepto en el caso de un cubo, que tiene el grupo de
simetría octaédrica más grande, del orden 48, que tiene como
subgrupos tres versiones de D
4h. El grupo de rotación es D
n del orden 2
n, excepto en el caso de un cubo, que tiene el grupo O de simetría más grande del orden 2
4, que tiene como subgrupos tres versiones de D
4.
El grupo de simetría D
nh contiene
inversión si n es par.
Polítopo prismática
Un
polítopo prismático es una generalización dimensión más alta de un prisma. Un polítopo prismático de n dimensiones se construye a partir de dos (n - 1) polítopos tridimensionales, traducidos a la siguiente dimensión.
El polítopo prismático de n-elementos se duplica a partir de los elementos polítopos (n − 1)- y luego creando nuevos elementos a partir del siguiente elemento inferior.
Tómese un polítopo-
n con elementos
fi caras-i (
i = 0, ..., n). Su prisma polítopo (
n + 1) tendrá
2fi + fi−1 i elementos. (Con
f−1 = 0,
fn = 1.)
Por dimensión:
- Tomar un polígono con n vértices y n aristas. Su prisma tiene 2n vértices, 3n bordes y 2 + n caras.
- Tomar un poliedro con v vértices, e aristas y f caras. Su prisma tiene 2v vértices, 2e + v aristas, 2f + e caras, y 2 + fceldas.
- Tomar un polícromo con v vértices, e aristas, f caras y c celdas. Su prisma tiene 2v vértices, 2e + v bordes, 2f + e caras, y 2c + f y 2 + c hiperceldas.
Polítopo prismático uniforme
Por dimensión:
- Un prisma 0 politópico es un segmento de recta, representado por un símbolo de Schläfli vacío {}.
- Un prisma politópico-1 es un rectángulo, formado a partir de la traslación de 2 segmentos de línea. Se representa como los el símbolo Schläfli producto {} x {}. Si se trata de un cuadrado, se puede reducir la simetría a: {} x {} = {4}.
 Ejemplo: Cuadrado, {} x {}, dos segmentos de recta paralelos, conectados por dos lados de segmentos de recta.
Ejemplo: Cuadrado, {} x {}, dos segmentos de recta paralelos, conectados por dos lados de segmentos de recta.
- Un prisma poligonal es un prisma de 3 dimensiones hecho a partir de dos polígonos trasladados, conectados por rectángulos. Un polígono regular {p} puede construir el prisma n-gonal uniforme representado por el producto {p} × {}. Si p = 4, con lados cuadrados simétricos, se convierte en un cubo: {4}×{} = {4, 3}.
- Un prisma poliédrico es un prisma de 4 dimensiones hecho por dos poliedros trasladados conectados por celdas de prisma de tridimensionales. Un poliedro regular {p, q} puede construir el prisma policórico uniforme, representado por el producto {p, q}×{}. Si el poliedro es un cubo, y los lados son cubos, se convierte en un teseracto: {4, 3}×{} = {4, 3, 3}.
- ...Los politopos prismáticos de orden superior también existen como productos cartesianos de dos politopos. La dimensión de un politopo es el producto de las dimensiones de los elementos. El primer ejemplo de esto existe en un espacio de 4 dimensiones llamado duoprisma como el producto de dos polígonos. Los duoprismas regulares se representan como {p}×{q}.
¡Un prisma tiene la misma sección en toda su longitud!
| Una sección es la forma que se obtiene cuando se corta un objeto de manera recta. |
 |
Una sección de este objeto es untriángulo...
... tiene la misma sección en toda su longitud...
... así que es un prisma triangular.
|
| |
| |
Intenta dibujar una forma en un trozo de papel (¡sólo con líneas rectas!),
ahora imagina que se extiende hacia arriba desde la hoja de papel,
¡eso es un prisma! |
¡Sin curvas!
Un prisma es oficialmente un poliedro, así que todas las caras tienen que ser planas. No puede haber caras curvas. Así que la sección será un polígono (una figura con lados rectos). Por ejemplo, si la sección fuera un círculo el objeto sería un cilindro, no un prisma.
Todos estos son prismas:










 menos.
menos.